Incertitudes dans le processus IAO
Des techniques de simulation intelligentes qui tiennent compte des incertitudes
L'ingénierie assistée par ordinateur (IAO) fait désormais partie intégrante du processus de production. L'impact de l'IAO a énormément augmenté au cours des dernières décennies et continuera à laisser son empreinte sur le processus de développement des produits à l'avenir. Avec l'émergence récente de matériels de plus en plus puissants, la simple simulation de modèles informatiques - souvent basés sur des éléments finis (finite elements en anglais, ou FE) - pour un produit ou un processus donné n'est plus le facteur limitant. Il suffit de penser à la détermination de la géométrie optimale d'une plaque de coupe interchangeable sur un tour, aux calculs thermiques pendant l'impression 3D ou au calcul de la contrainte résiduelle après le tréfilage. Les progiciels modernes tels que Siemens NX, Ansys ou Abaqus fournissent une solution en un instant.

balayer les incertitudes à un stade précoce
Pourtant, les résultats calculés ne sont pas toujours fiables lorsqu'ils sont comparés aux valeurs mesurées. La raison en est que les calculs sont souvent basés sur des valeurs moyennes pour certains paramètres très variables, tels que les propriétés des matériaux, les propriétés thermiques, les caractéristiques géométriques, etc. De plus, de nombreux modèles informatiques sont des suppositions éclairées de la réalité, basées sur les connaissances spécialisées et spécifiques au domaine de l'ingénieur qui effectue les calculs.
Dans des conditions réelles, les variations des hypothèses pour ces paramètres peuvent fortement influencer le résultat du calcul. C'est pourquoi, ces dernières années, la prise en compte des incertitudes à un stade précoce du processus de conception a suscité un intérêt croissant. Une meilleure compréhension de la manière dont ces incertitudes influencent le résultat d'un calcul peut garantir des résultats plus fiables, de sorte que l'IAO restera un outil puissant au cours du processus de production.
Pour obtenir un résultat précis, il est nécessaire d'inclure toutes les sources d'incertitude dans le calcul. Cela peut à son tour augmenter considérablement le temps de calcul total. Au lieu d'un seul calcul IAO/FE, on effectue un grand nombre de calculs IAO/FE similaires, chacun avec des valeurs légèrement différentes pour les paramètres. Dans les méthodes de calcul classiques qui peuvent gérer l'incertitude, le nombre d'appels à un tel calcul IAO/FE croît de façon exponentielle avec le nombre d'incertitudes. Dans les modèles d'ingénierie complexes, où il y a souvent des dizaines, voire des centaines de paramètres incertains, ces méthodes deviennent rapidement inutilisables. Ce phénomène est également connu sous le nom de "malédiction de la dimension". D'un point de vue industriel, il est donc très important de développer des méthodes de calcul efficaces dont le coût de calcul ne dépend pas ou peu du nombre d'incertitudes considérées.

méthode de Monte Carlo
Un exemple d'une telle technique de calcul efficace est la méthode de Monte Carlo, ou la méthode du joueur de fléchettes ivre. Imaginez qu'un joueur de fléchettes lance trois coups sur un jeu de fléchettes. Par exemple, le joueur de fléchettes peut marquer 150 points - trois fois 50 - lorsqu'il lance trois fois dans la bulle. Mais, comme le joueur de fléchettes a trop bu, les fléchettes n'atterrissent pas toujours dans la bulle, mais dans des positions aléatoires sur la cible. Nous pouvons alors nous demander quel est le nombre attendu de points que le joueur de fléchettes marquera lorsqu'il lancera une fléchette trois fois. Pour le déterminer, nous pouvons mettre en place une expérience. Nous laissons le joueur de fléchettes lancer trois fléchettes un grand nombre de fois sur la cible et nous enregistrons le score à chaque fois. Le score attendu est alors le score moyen du joueur de fléchettes (c'est la somme du score total après toutes les répétitions divisée par le nombre total de répétitions).
L'idée d'estimer le score attendu comme une moyenne sur un grand nombre de répétitions est la base de la méthode de Monte Carlo. Or, il s'avère que le nombre de fois que nous devons répéter l'expérience pour prédire le résultat avec une certaine précision ne dépend pas du nombre de fléchettes utilisées par jeu. En d'autres termes, en choisissant une valeur aléatoire pour chaque fléchette (chaque paramètre), le nombre total de répétitions (le nombre de calculs) ne dépend pas du nombre de fléchettes (le nombre de paramètres).
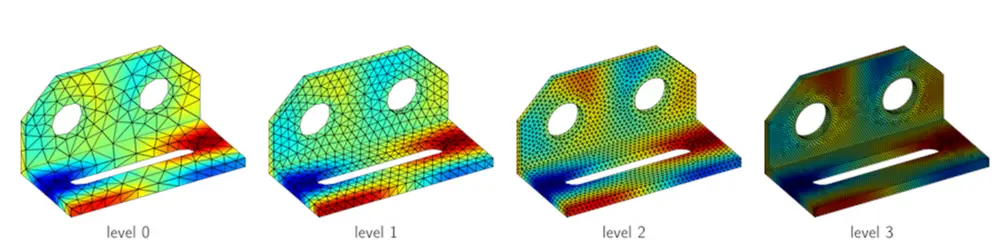
Plus il y a d'éléments, plus les résultats sont précis, mais plus les calculs sont coûteux
Méthodes multi-niveaux
Malheureusement, dans la pratique, le nombre de calculs IAO/FE requis par la méthode du joueur de fléchettes ivre est encore beaucoup trop important pour être d'une utilité pratique. C'est pourquoi on utilise souvent des méthodes à plusieurs niveaux (multilevel en anglais, ou ML) pour réduire encore le coût du calcul. Ces méthodes sont basées sur l'approche par éléments finis du processus ou du produit, par exemple pour une pièce de machine. Dans la méthode des éléments finis, la pièce est divisée en un nombre fini d'éléments aux formes géométriques plus simples, comme des rectangles et des triangles (2D) ou des cubes et des tétraèdres (3D). Les lois physiques peuvent alors être rapidement écrites pour cette géométrie simple.
Un exemple d'une telle technique de calcul efficace est la méthode de Monte Carlo, ou la méthode du joueur de fléchettes ivre

Le comportement de l'ensemble de la pièce peut alors être calculé à partir du comportement des éléments individuels. Plus le nombre d'éléments est élevé, plus le calcul est complexe, mais aussi plus le résultat est précis. C'est là que réside la puissance des méthodes ML: d'abord, un grand nombre de calculs de Monte Carlo bon marché mais imprécis sont effectués avec peu d'éléments, puis un nombre toujours plus petit de calculs de Monte Carlo plus coûteux mais plus précis sont effectués avec toujours plus d'éléments, pour corriger les calculs bon marché précédents. Comparez cela avec la méthode habituelle du joueur de fléchettes ivre, où tous les calculs sont effectués avec le même grand nombre d'éléments.
Les calculs d'incertitude avec la méthode ML sont souvent plusieurs dizaines, voire centaines de fois plus rapides que les autres méthodes, qui n'utilisent qu'une seule approche par éléments finis très précise. Cette accélération impressionnante profite au processus de conception: effectuer un calcul d'IAO avec prise en compte de l'incertitude n'est qu'un petit multiple d'un calcul IAO/EF classique non basé sur l'incertitude. Les méthodes ML mettent donc des résultats plus fiables à la portée de l'ingénieur concepteur.
Concept robuste
Ces calculs moins coûteux sont principalement utiles pour réaliser ce que l'on appelle un concept robuste. Il s'agit d'un concept qui tient compte de l'incertitude. Au lieu d'opter pour une conception qui offre les meilleures performances possibles (par exemple, le moindre coût, la moindre déflexion ou la moindre dilatation thermique), on recherche la conception qui offre de bonnes performances pour une large gamme de valeurs de paramètres différentes. Pensez à une plaque de coupe qui s'use peu dans une large plage de vitesses de coupe et pour différents matériaux. Ou encore, pensez à concevoir le mandrin d'un tour en omettant le plus de matériau possible pour gagner du poids, mais en restant suffisamment solide pour des forces de serrage variables. Dans tous ces cas, une conception IAO robuste vous permet de livrer un produit sur lequel le client peut compter.

